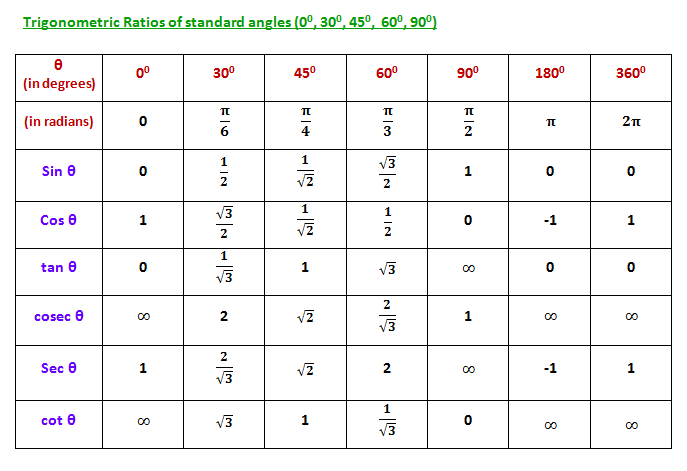
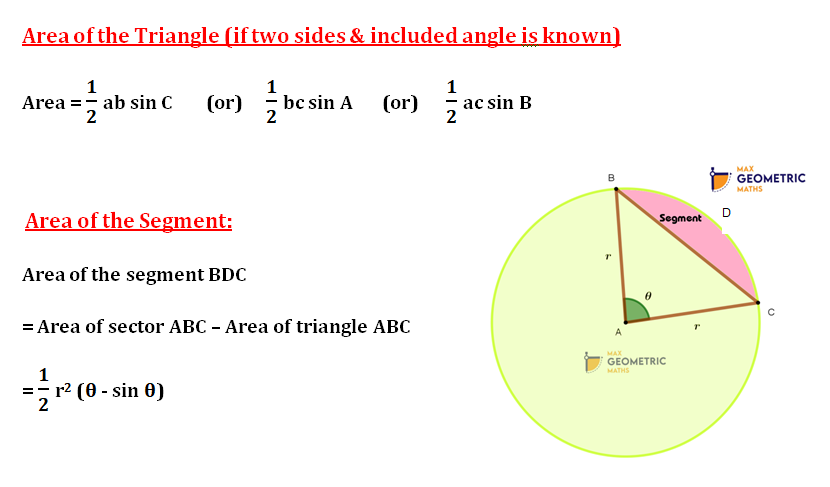
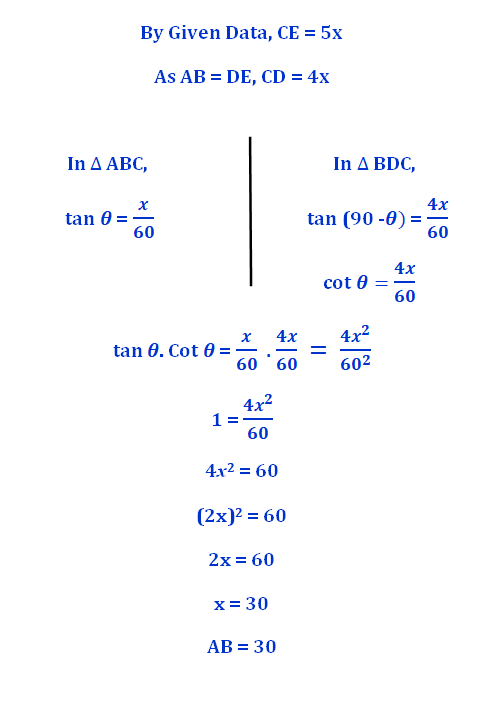Trigonometry, the branch of mathematics concerned with specific functions of angles and their application to calculations. There are six functions of an angle commonly used in trigonometry. Their names and abbreviations are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). These six trigonometric functions in relation to a right triangle are displayed in the figure. For example, the triangle contains an angle A, and the ratio of the side opposite to A and the side opposite to the right angle (the hypotenuse) is called the sine of A, or sin A; the other trigonometry functions are defined similarly. These functions are properties of the angle A independent of the size of the triangle, and calculated values were tabulated for many angles before computers made trigonometry tables obsolete.
Trigonometry developed from a need to compute angles and distances in such fields as astronomy, mapmaking, surveying, and artillery range finding. Problems involving angles and distances in one plane are covered in plane trigonometry. Applications to similar problems in more than one plane of three-dimensional space are considered in spherical trigonometry.
Basics
Trigonometry means Trigonon (“triangle”) and metron (“to measure”).
Trigonometry is a branch of mathematics that deals with functions of angles and their applications.
It gives the relation between sides & angles of a triangle.
It has wide range of applications in various branches of Mathematics, Physics, Engineering, criminology, etc.,
Six Trigonometric functions are:
Sine
Cosine
Tangent
Cosecant
Secant
Cotangent
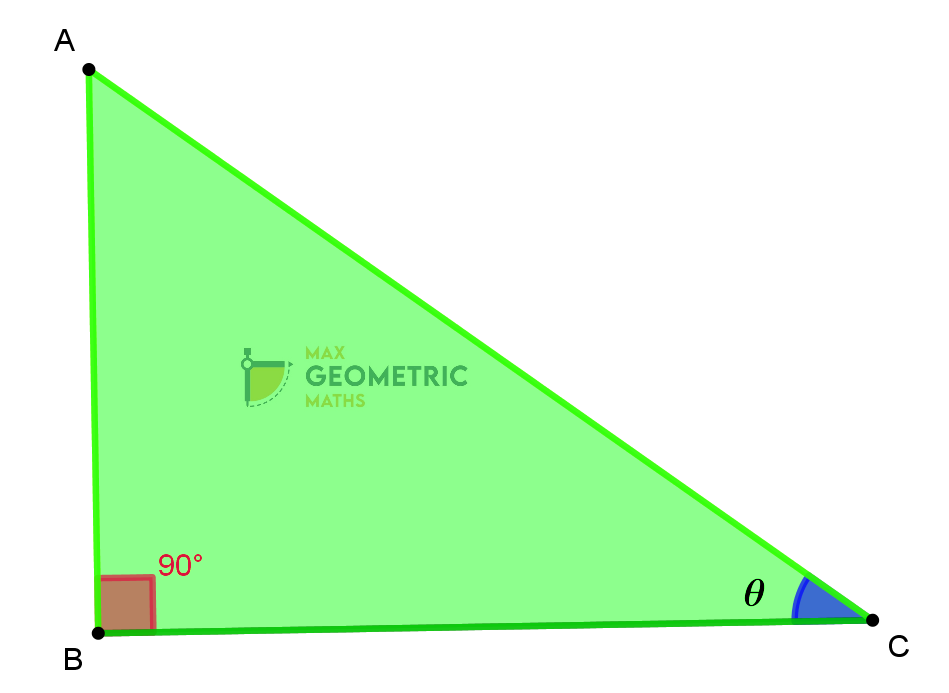
In a right angled triangle ABC,
Hypotenuse
The side opposite to the right angle (90
Opposite Side
The side opposite to angle ‘ θ’. = AB
Adjacent Side
The side adjacent to angle ‘ θ’.= BC






Author’s Creation in Trigonometry
1. Question:
HUNTER-BIRD PROBLEM
A hunter (his height is 2 meters) was standing at a distance of 24 meters from a pole of height 10 meters, aiming his bow and arrow at a bird sitting on the top of the pole. The angle of elevation of the bird from his eyes was x°. The hunter knew that on hearing the sound of the release of the arrow from the bow, the bird would suddenly fly perpendicular to the ground and therefore, he had to shoot his arrow at a degree higher than x° so that the arrow would hit the bird while flying perpendicularly above the pole. The speed of his arrow was 12 meters per second. He aimed his arrow at 2x° and released it. The bird on hearing the release -sound flied above the pole perpendicularly but it was hit by the arrow. Find the speed (meters per second) at which the bird flied.
Problem created by
Dr.M.Raja Climax, FOUNDER CHAIRMAN, CEOA
2. Question:
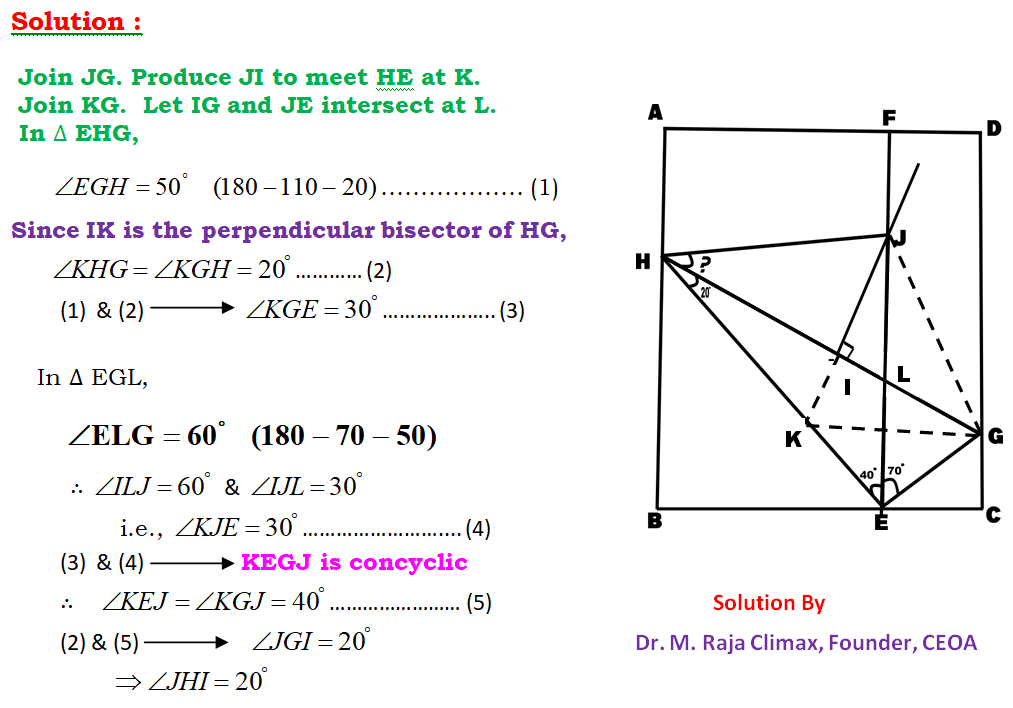
QUARANTINE PROBLEM
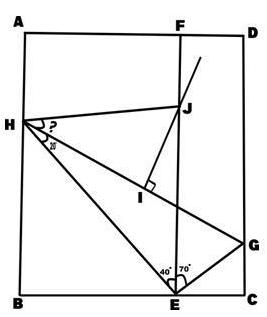
A house was to be quarantined by sealing its entrance. The entrance was a rectangular frame ABCD as shown in the picture. First, the point E was chosen on BC. From E a wooden stick was perpendicularly affixed touching AD at F. Then, from E another wooden stick was affixed touching DC at G such that <FEG = 70°. Another wooden stick was affixed at E touching AB at H such that <HEF = 40°. Another wooden stick was nailed joining HG. <EHG = 20° Then the midpoint of HG was located at I. From I, another wooden stick was perpendicularly affixed and crossing EF at J. Another wooden stick was affixed joining JH. Find the measurement of <JHI.
Problem created by
Dr.M.Raja Climax, FOUNDER CHAIRMAN, CEOA
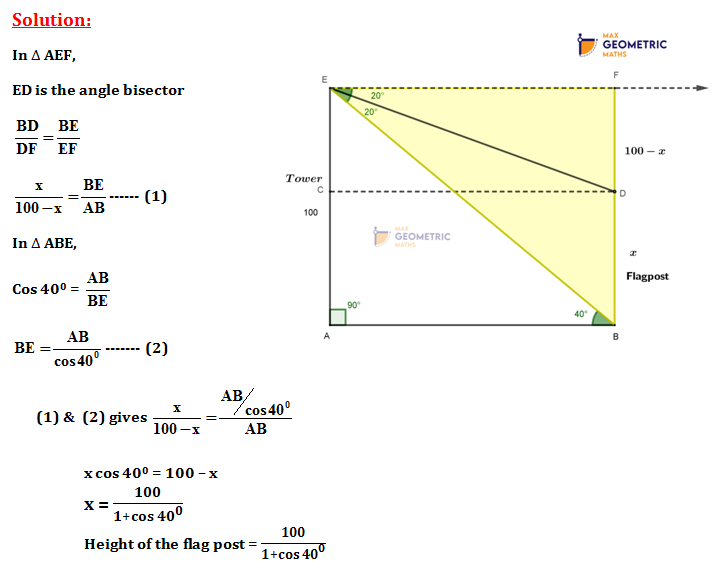
3. Question:
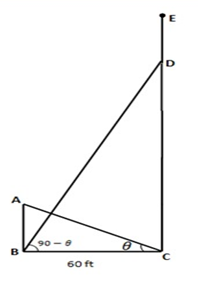
A tower and a lamp post are standing with a distance of 60ft between them. A flag post is standing on the top of the tower. The flag post and the lamp post are of equal heights. The ratio between the height of the lamp post and that of the tower (including the flag post) is 1: 5. The angle of elevation of the top of the lamp post from the bottom of the tower is @ degree. The angle of elevation of the bottom of the flag post (top of the tower) from the bottom of the lamp post is (90 — @) degree. Find the height of the lamp post.
AB = Lamp post
CD = Tower
DE = Flag post
AB=?
Rules: Formula / Theorem learnt after X std should not be used.
Clark's or other Tables should not be used.
- Dr.M.Raja Climax, Founder Chairman
4. Question:
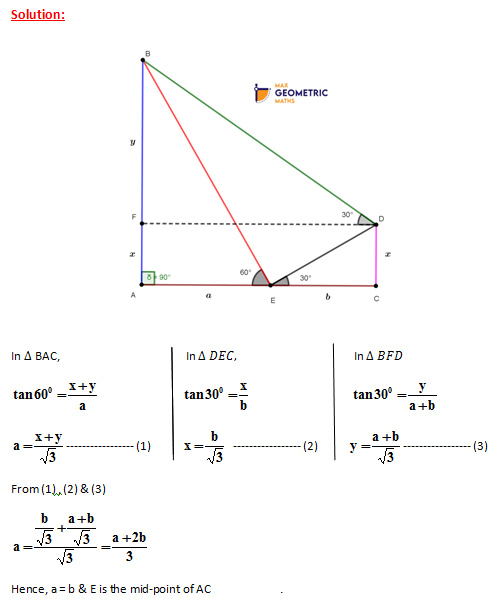
AB & CD are a tower & a pole respectively standing on a straight road. A & B are the bottom & top of the tower respectively and C &D are the bottom & top of the pole respectively. E is a point on the same road lying between A & C. The angles of elevation of B & D from E are measured as 600 & 300 respectively. The angle of elevation of B from D is measured as 300. Then, prove that E is the mid-point of AC.
5. Question:
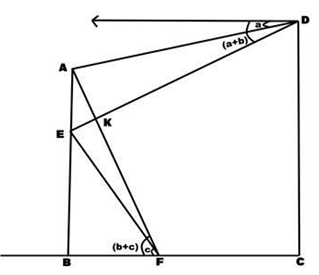
A tower AB (with a flag post AE on its top) and a light house CD are standing apart as shown in the picture. F is a point on the straight line joining B & C. AF and DE are joined with the help of ropes intersecting each other at K. From F, the angles of elevation of E& A are measured as c° & (b+c)° respectively. From D, the angles of depression of A & E are measured as a° & (a+b)° respectively. ED: AF = 8:7, EK: KD = 1:3. Find the ratio of AK: KF.
- Dr.M.Raja Climax
6. Question: