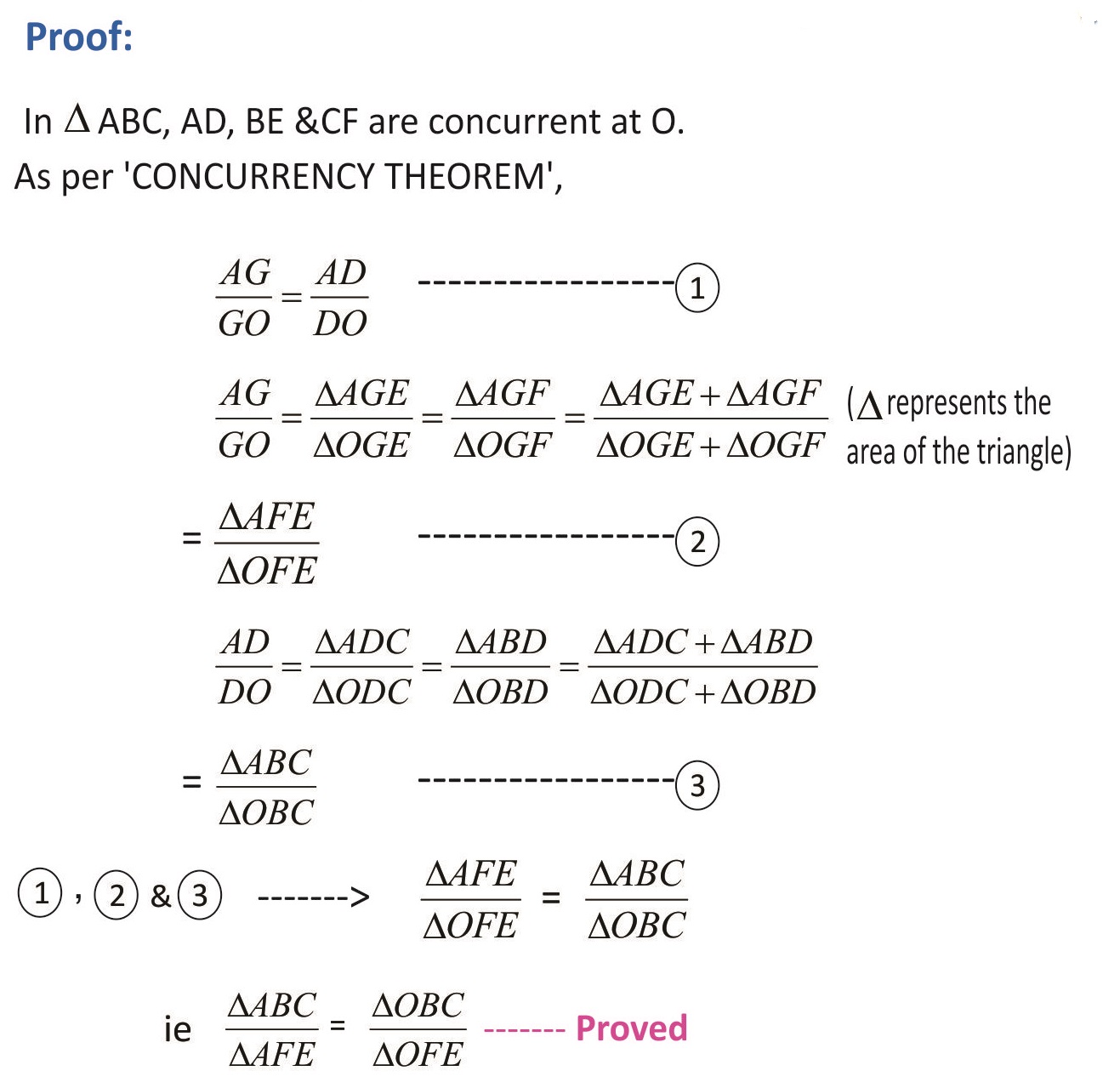
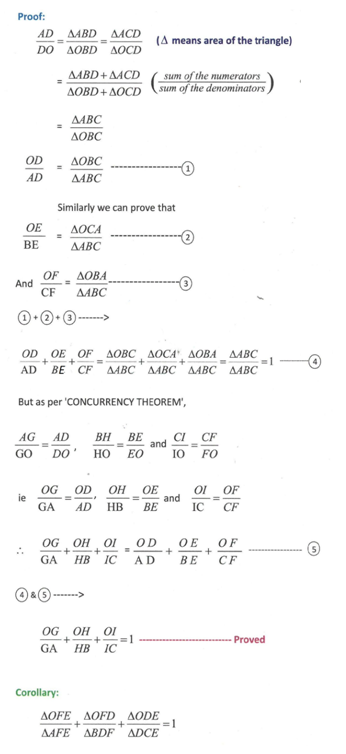
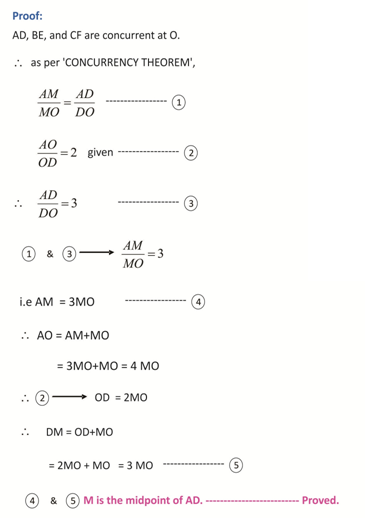
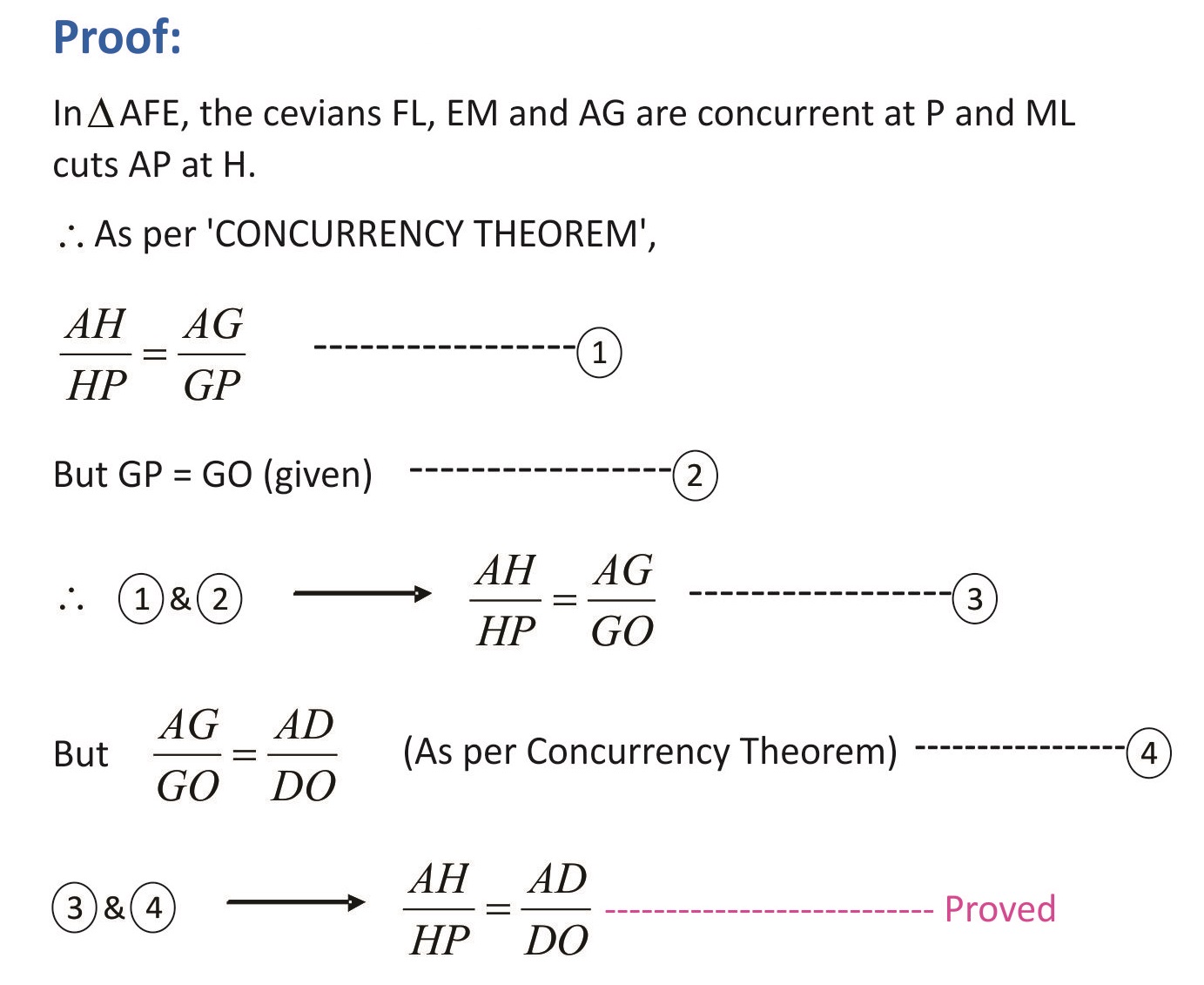
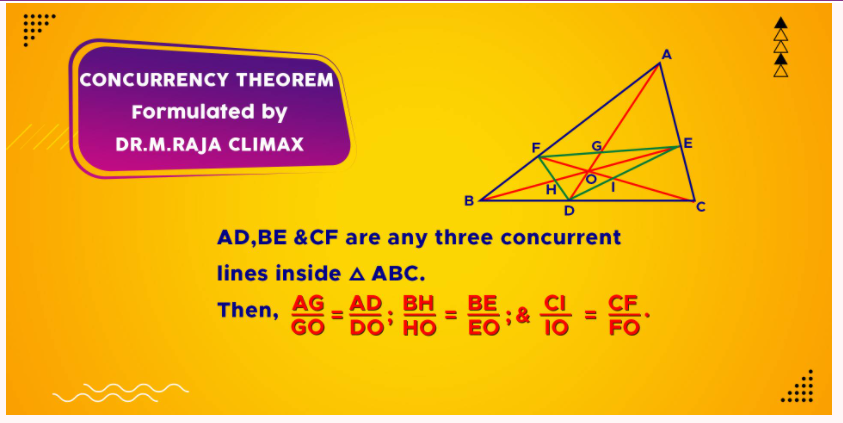
The Concurrency Theorem brings out a useful result for the concurrent lines drawn inside a triangle. The said result is a further development from the Menelaus theorem. The Concurrency Theorem employs Menelaus theorem to prove the said interesting result. This theorem has been named as the CONCURRENCY THEOREM for the simple reason that it springs out from the concurrent lines drawn from the three vertices of a triangle. The concurrent lines drawn from the vertices are geometrically known as ‘cevians’. Though this result (the Concurrency Theorem) is already in existence in the arena of Geometry as a simple feature of a quadrangle with a corollarical significance, the same is presented here in a new form and projected with a new proof. Moreover, based on the concurrency theorem 25 beautiful riders have been developed & given here.
Concurrency Theorem
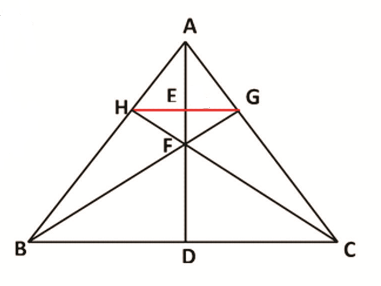
Converse of Concurrency Theorem

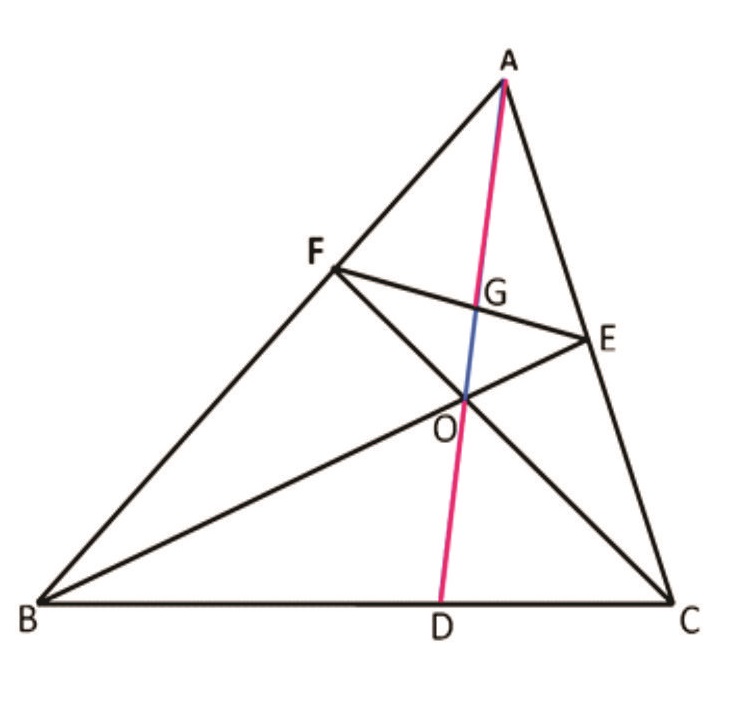
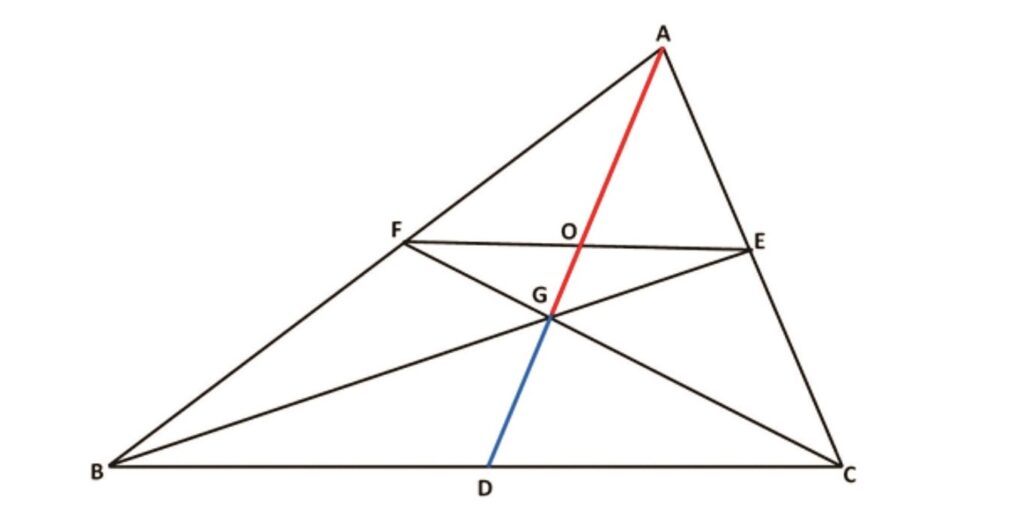
Rider : 1
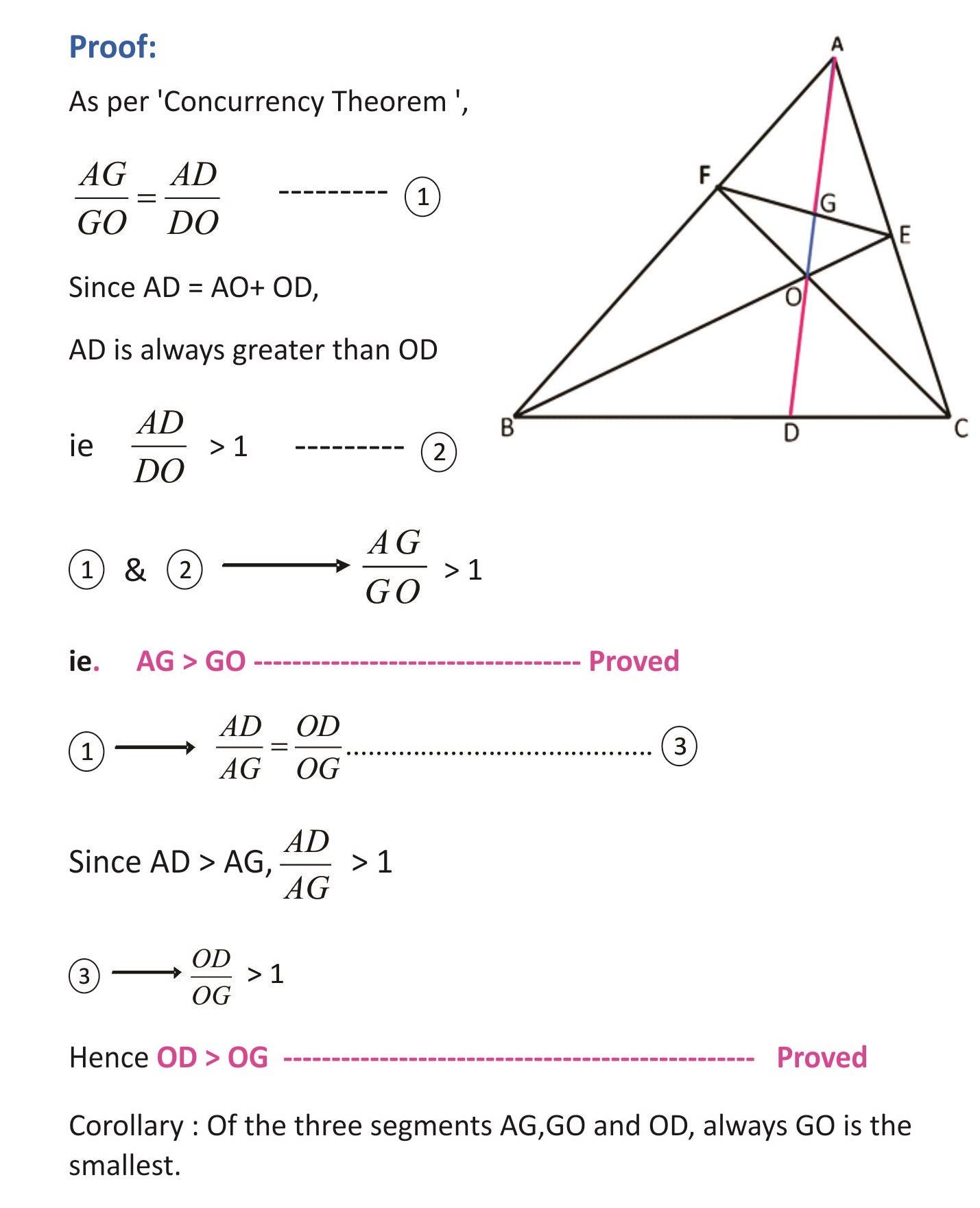
In Δ ABC, AD, BE and CF are cevians concurrent at O meeting BC, CA and AB at D, E and F respectively. EF and AD cuts at G. Prove that AG and OD are always greater than GO.
Rider : 2
Rider : 3
In ΔABC, AD is the bisector of angle A meeting BC at D. O is the mid-point of AD. BO and CO are produced to meet AC and AB at E and F respectively and EF cuts AD at G. The line drawn perpendicular to AD at O meets AB and AC respectively at H and I. Prove that G is the centroid of triangle AHI.
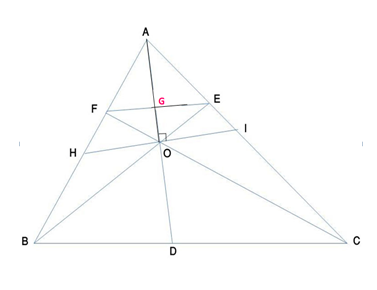
Rider : 4
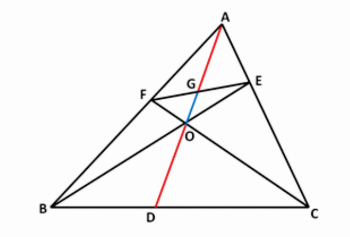
Rider : 5
AB is a straight line. X is a point on AB lying between A and B and dividing AB in a particular ratio. Find out the point Y on AB produced which divides AB externally in the same ratio ie. such that AX / XB = AY / YB
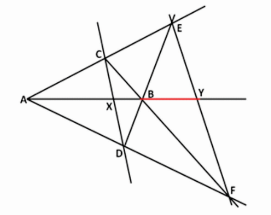
Rider : 6
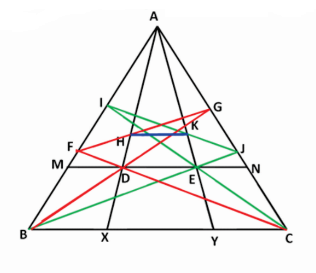
Rider : 7
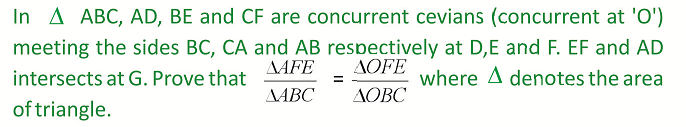
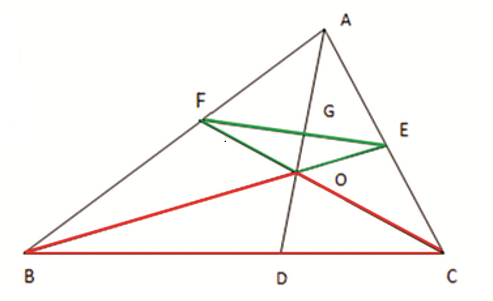
Rider : 8
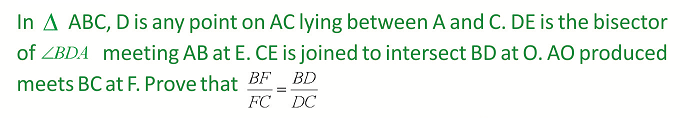
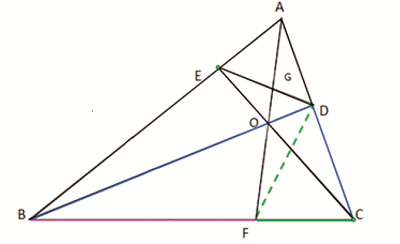
Rider : 9

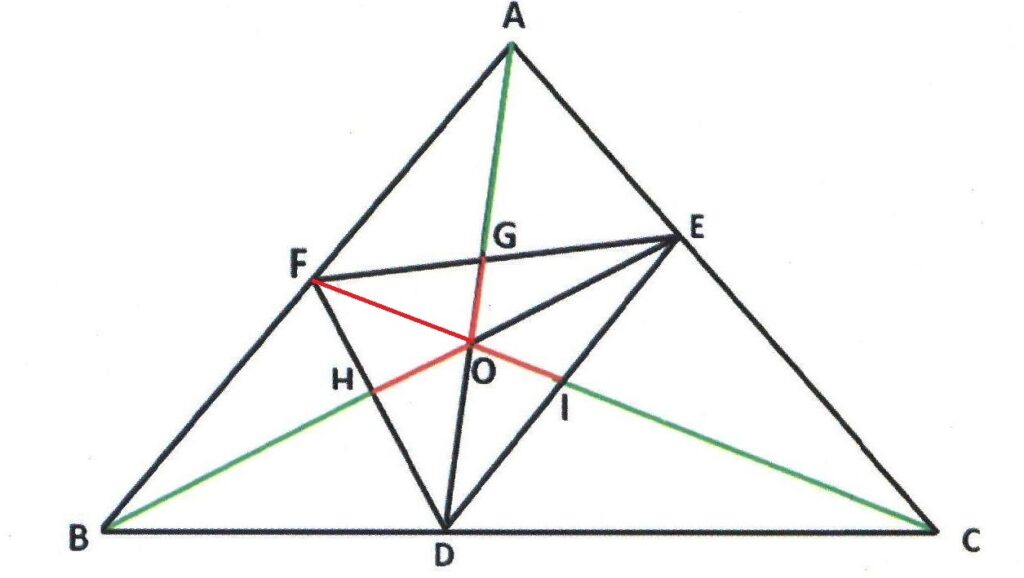
Rider : 10

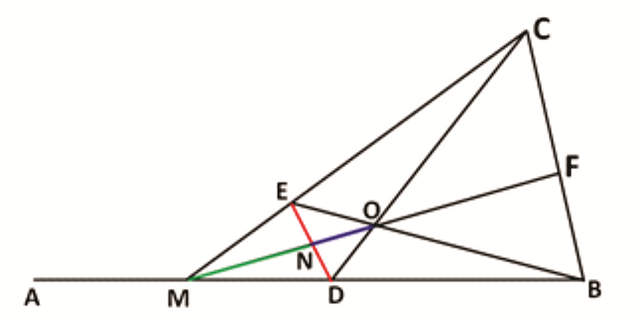
Rider : 11

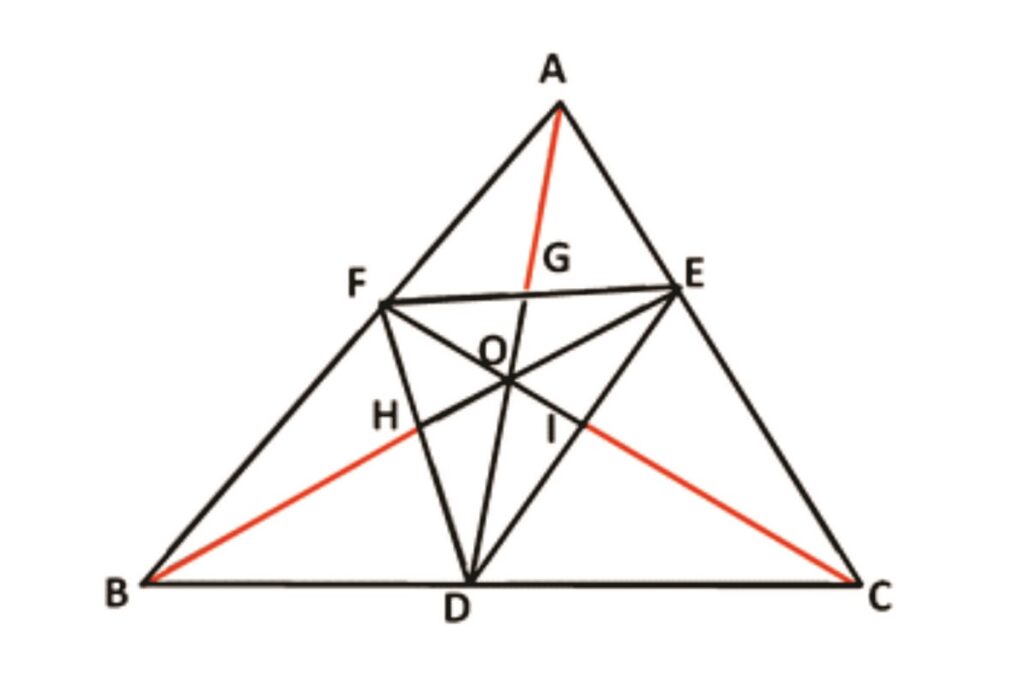
Rider : 12
In Δ ABC, AD, BE and CF are Cevians concurrent at ‘O’. FE is produced to meet BC produced at G. AD is produced and H is a point on AD produced. BE is produced to meet HC produced at I. BH and FC are produced to meet at J. Prove that J, G and I are collinear.
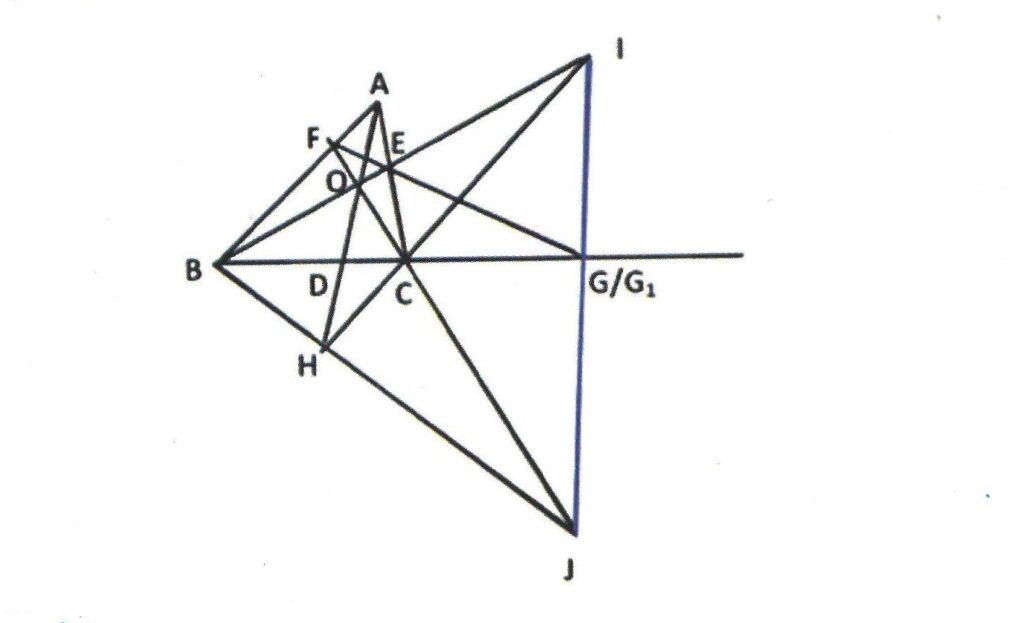
Rider : 13

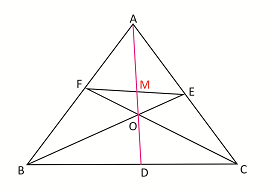
Rider : 14

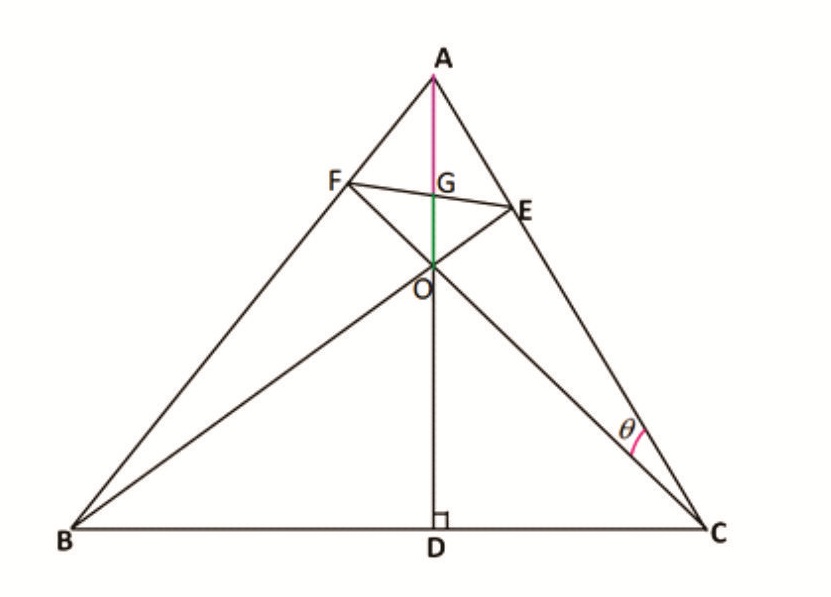
Rider : 15

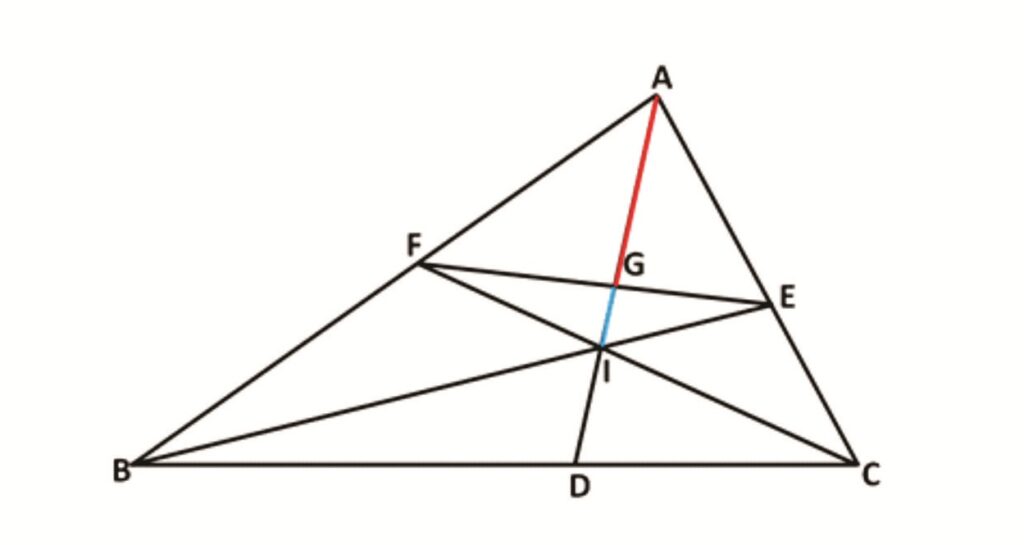
Rider : 16

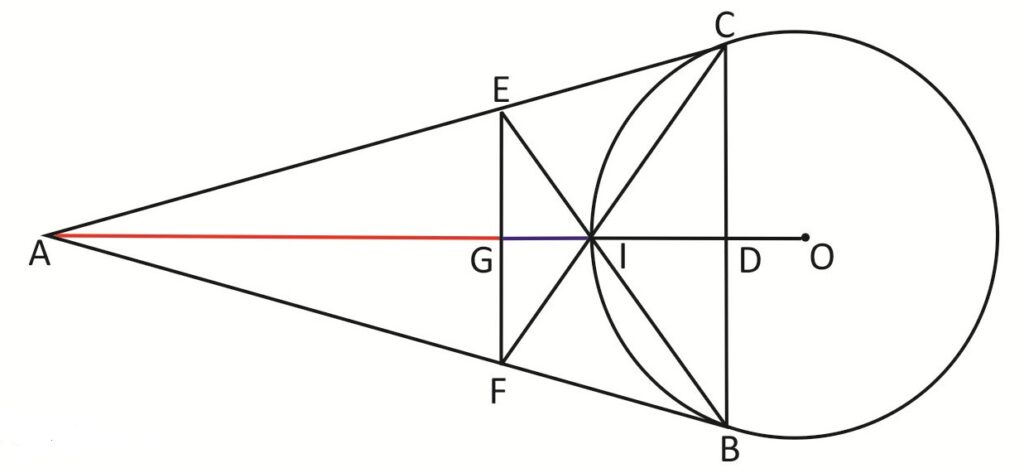
Rider : 17
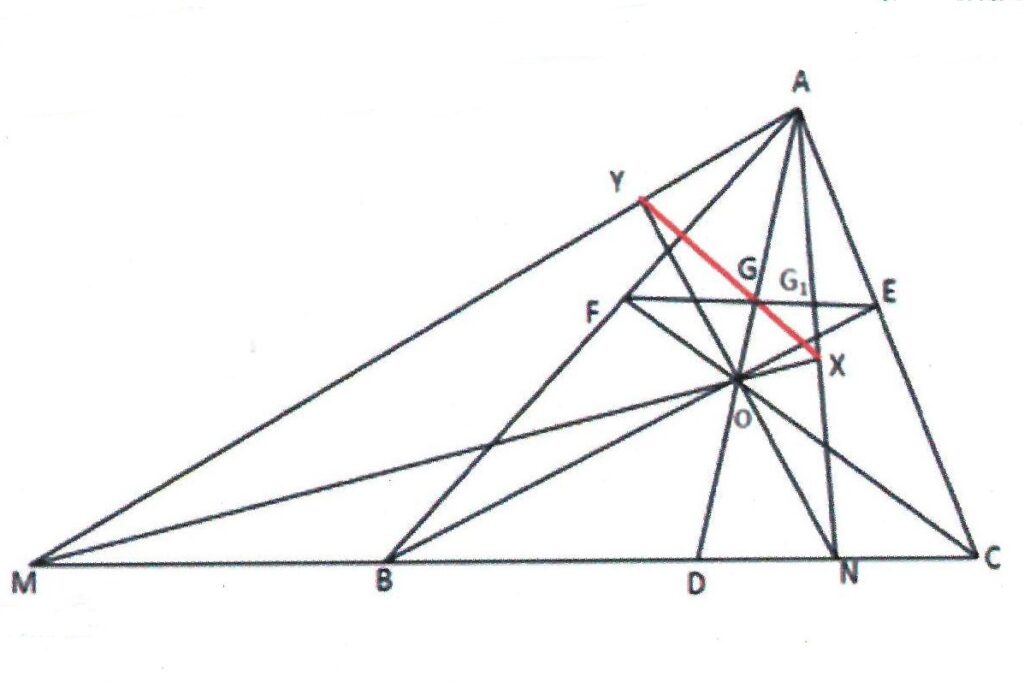
Rider : 18

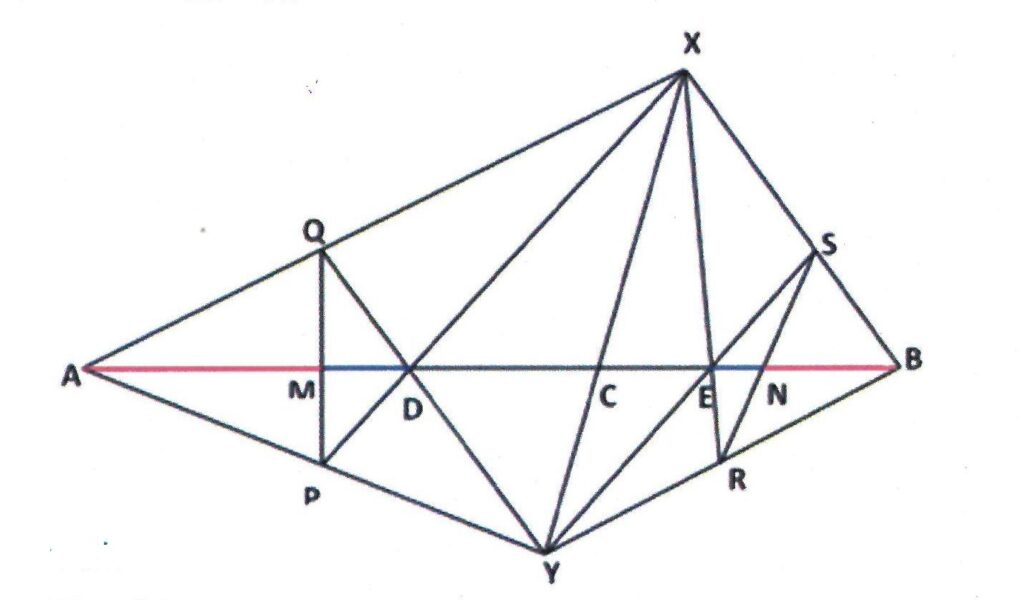
Rider : 19
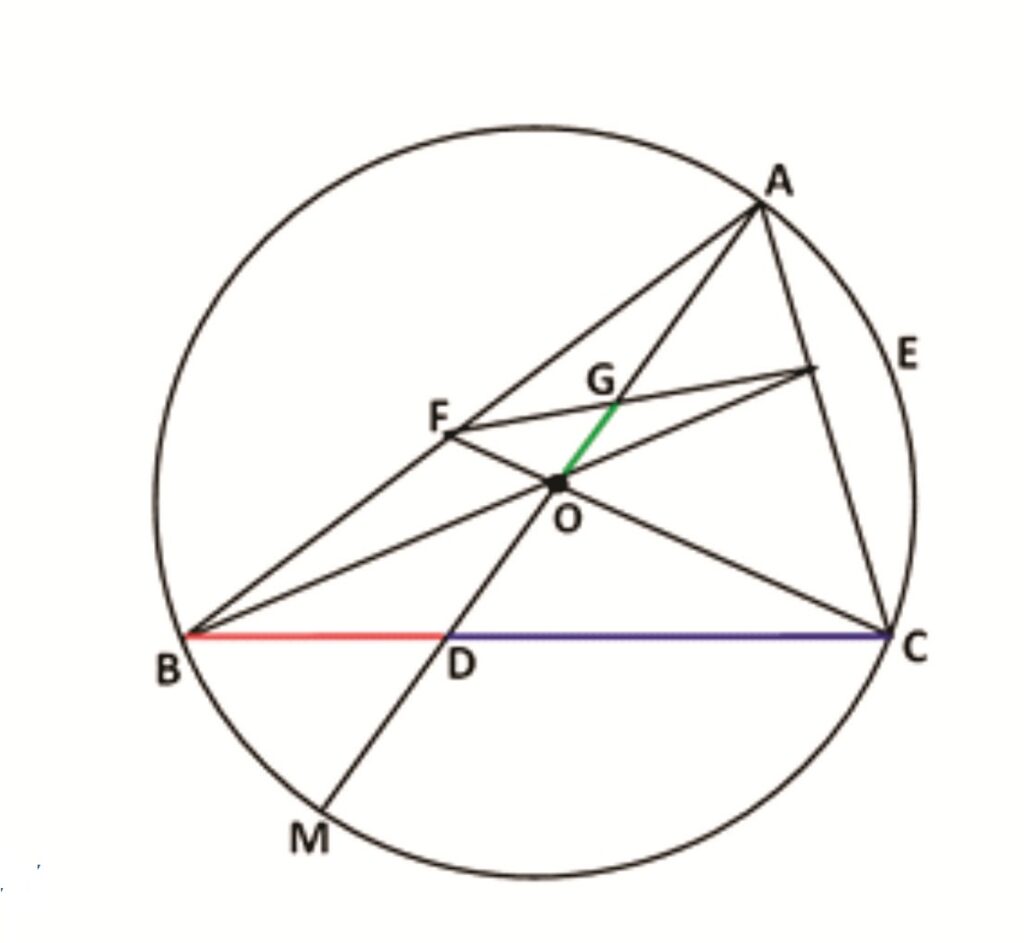
Rider : 20

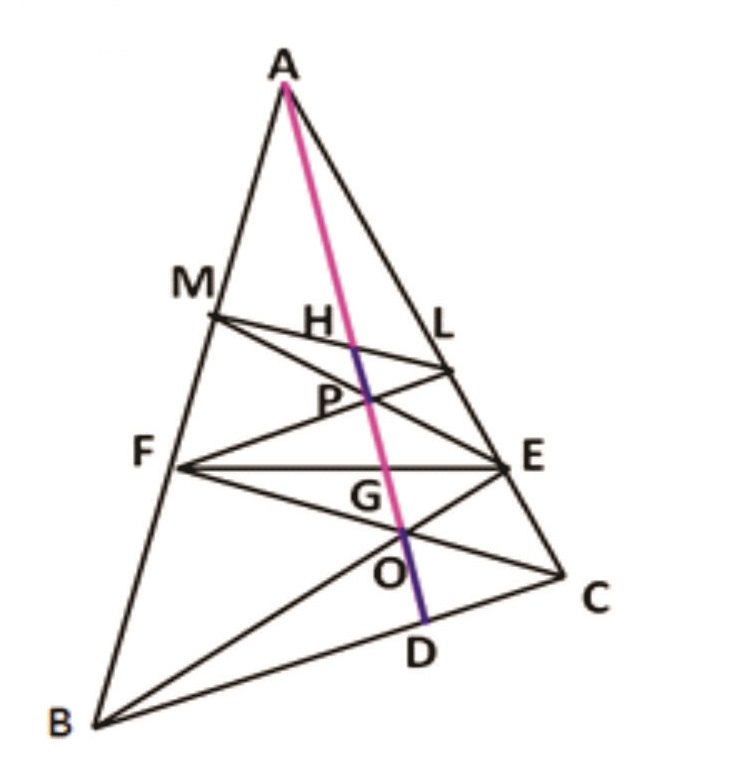
Rider : 21(a)
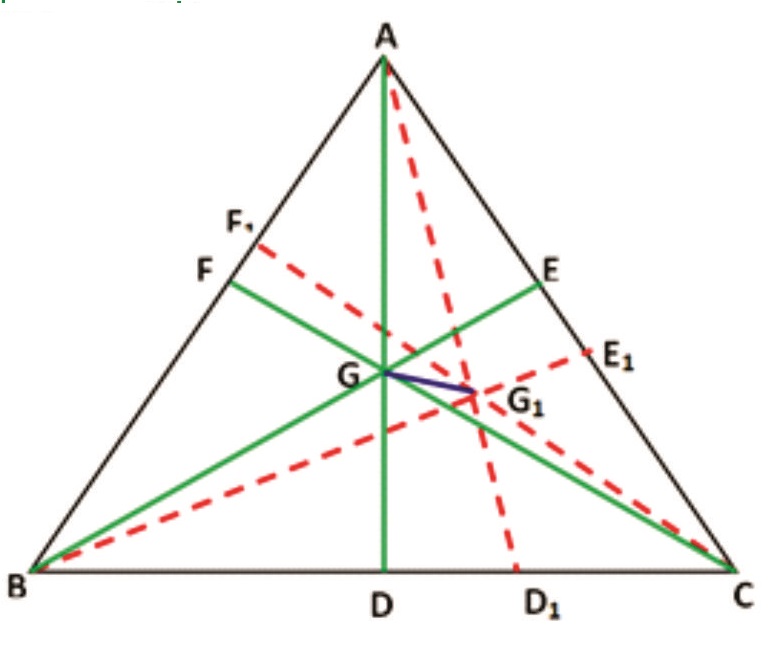
Rider : 21(b)
AB is a straight line segment with midpoint M. AX and BY are straight lines drawn through A and B cutting each other at O. G and H are points on AO and BO respectively such that OA = 4OG and OB = 4OH. MG and MH are joined and produced to cut BY and AX at D and E respectively. AD and BE meet at C. Prove that O is the centroid of the Δ ABC.
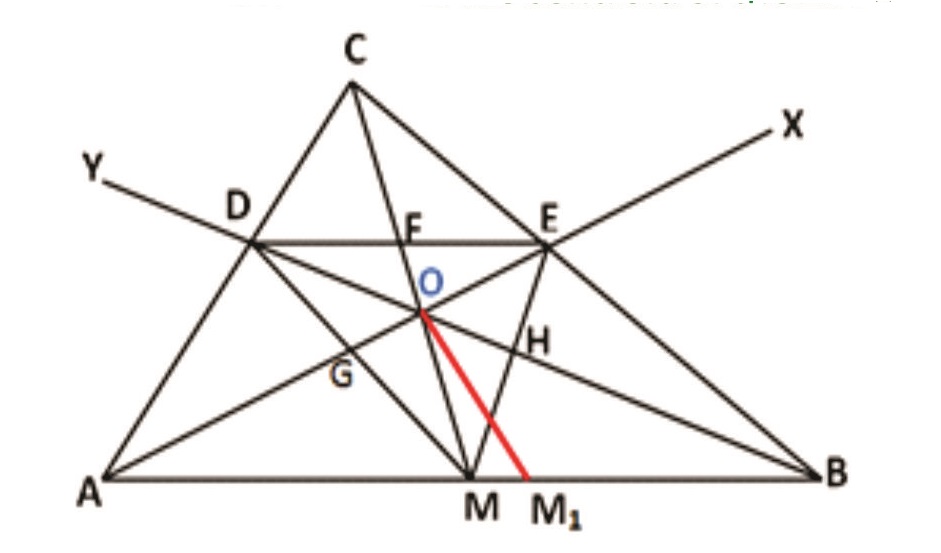
Rider : 22
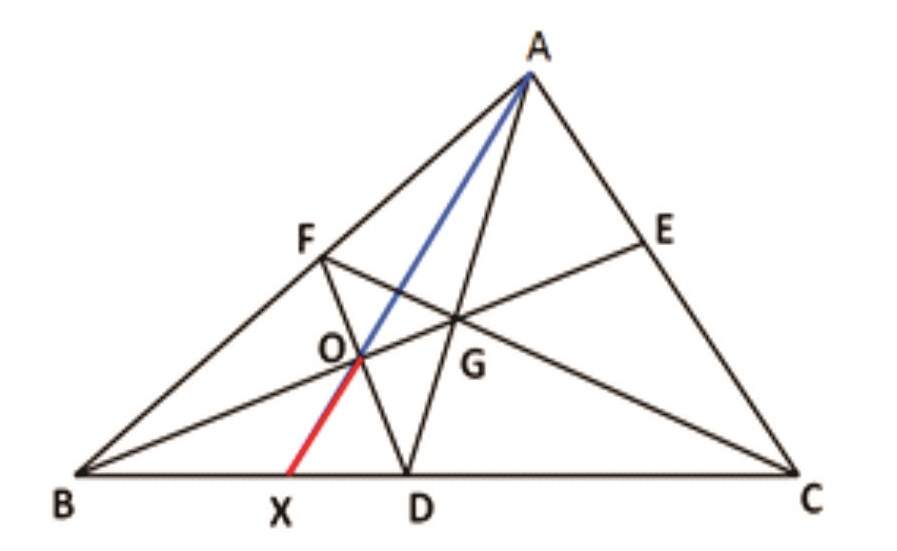
Rider : 23
AD, BE and CF are cevians of ΔABC concurrent at O. FE cuts AD at G. A line is drawn through G parallel to BE to cut AC at P and DE produced at Q. AQ and FE are produced to meet at R. DR is joined to cut AC at S. Prove that DSR is parallel to GQ. Hence, deduce that S is the midpoint of DR.
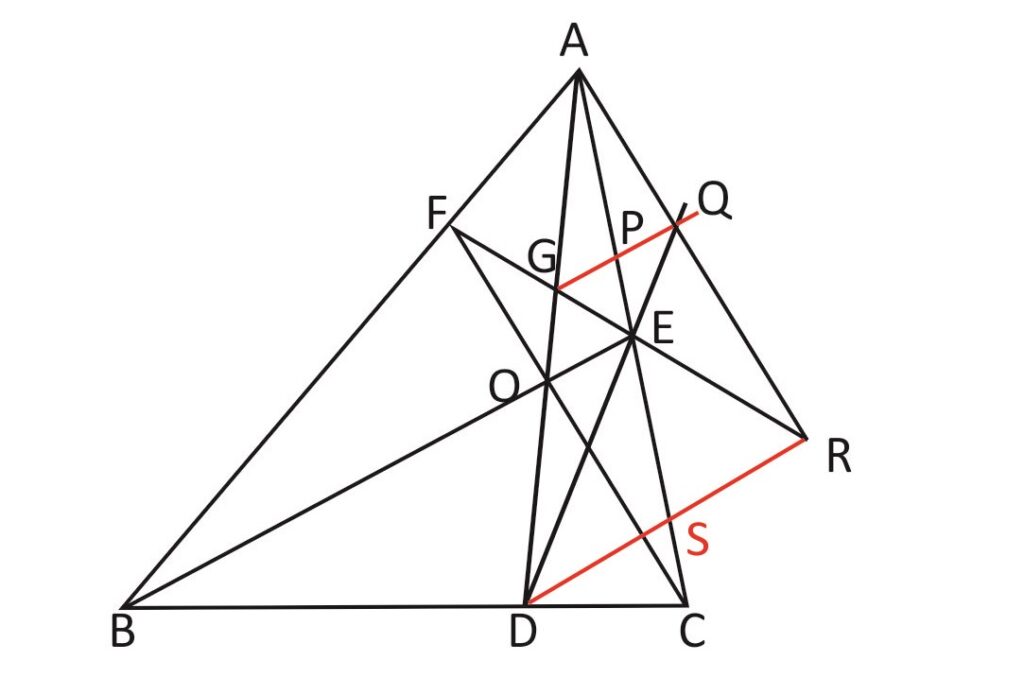
Rider : 24

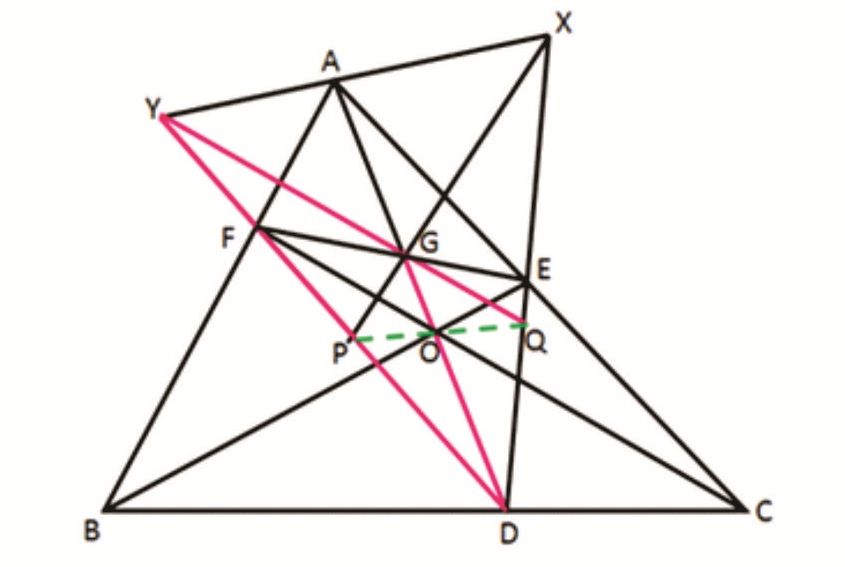
Rider : 25
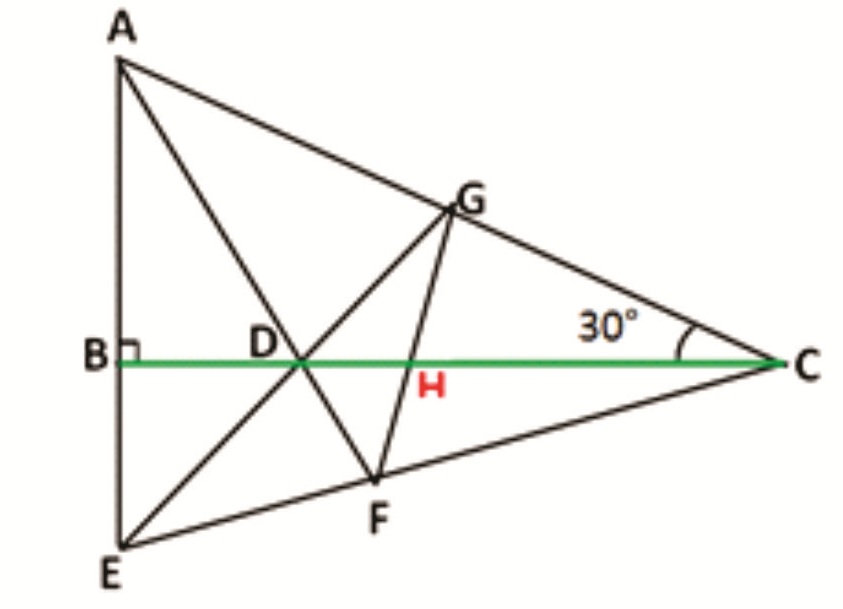
ΔABC is a right angled triangle with right angle at B and 30° at C. AD is the bisector of meeting BC at D. E is a point on AB produced. EC cuts AD produced at F. ED produced meets AC at G and GF and BC cut at H. Prove that H is the midpoint of BC.